layout: post title: “pytorch深度学习” date: 2021-05-27 description: “”
tag: pytorch 深度学习
概念
-
机器学习和深度学习原理:
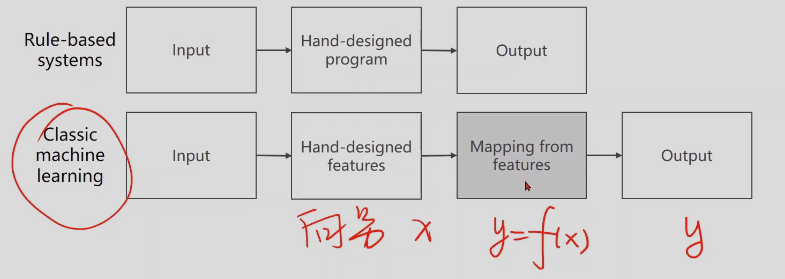

算法,是基于人类指定规则,
机器学习是Input经过人类手动提取特征(真正的输入x),然后mapping from features是完成y对x的函数映射,output是y
表型学习是features的提取也可以学习,自动提取
深度学习,是把数据输入的最简单特征直接作为输入,然后接入额外的层,提取特征
-
维度诅咒:
维度越多,对数据需求越大。
-
Back Propagation(计算图)反向传播算法
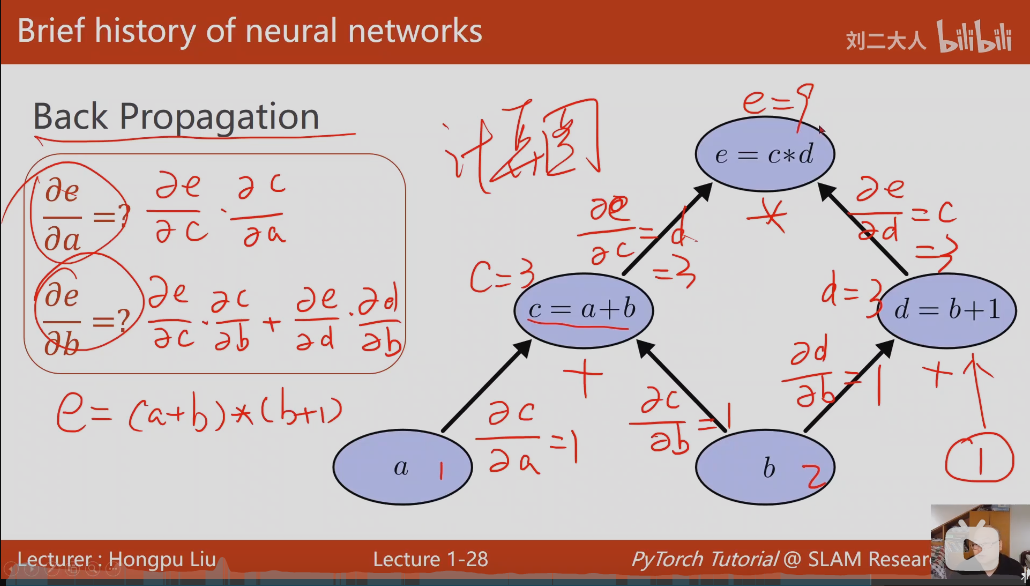
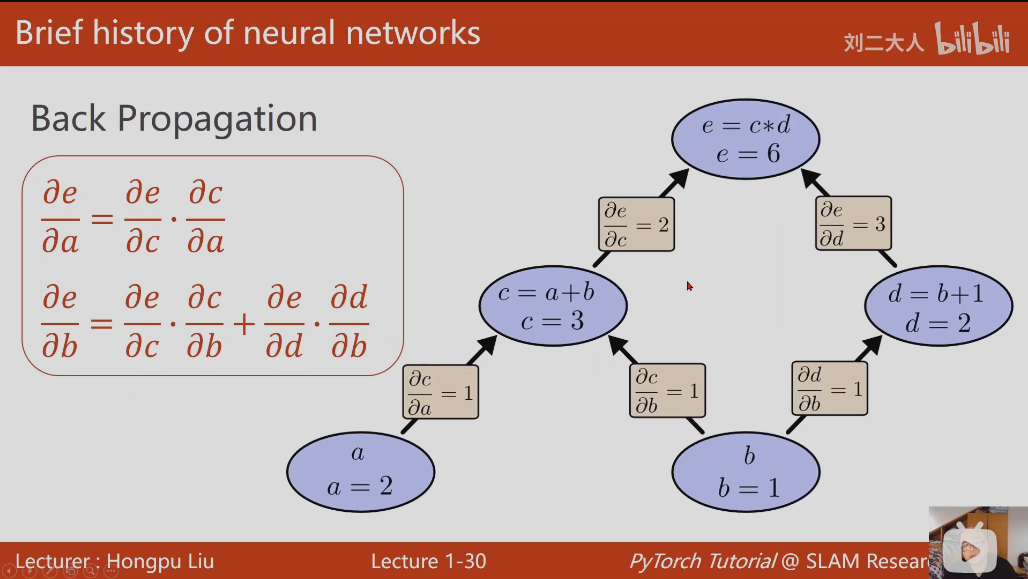
单条路径: e对a的导数,等于a到e路径上所有偏导的乘积,
多条路径: e对b的导数,等于两条路径偏导乘积的和
-
需要线性代数和概率论
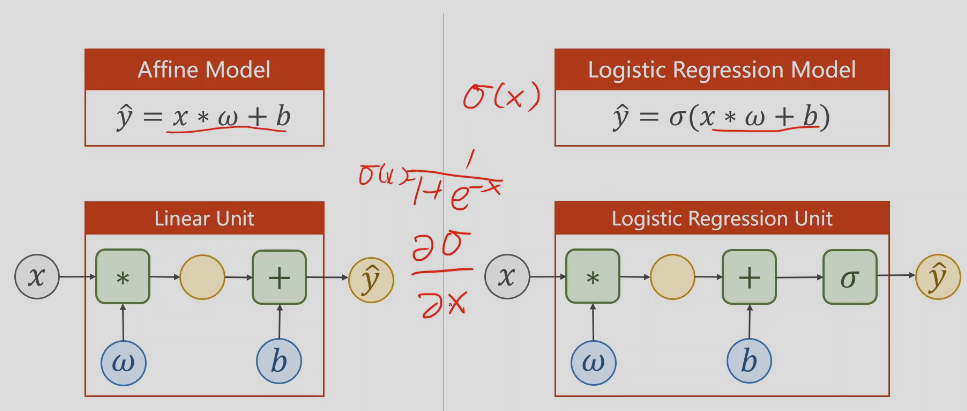
线性模型
-
准备数据集 dataset
-
选择模型model(随机森林、knn)
-
training
-
inferring OR predicting
-
模型评估–损失loss
MSE(平均方差损失)

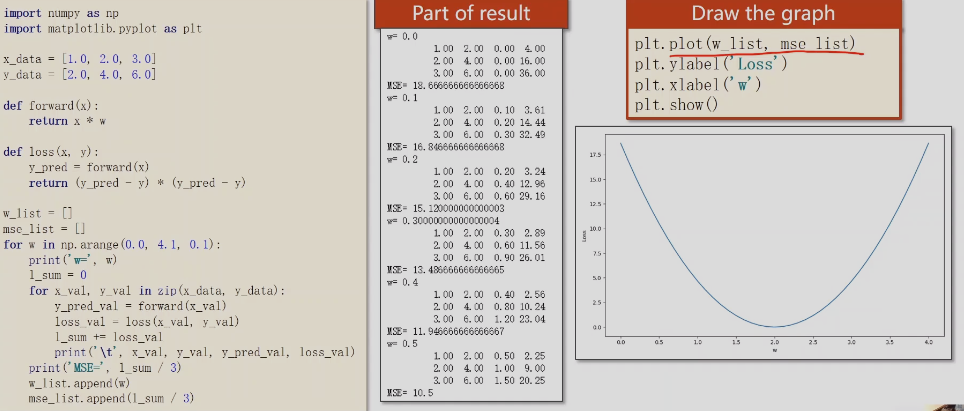

注意:
模型训练过程中实时的画一些可视化图,比如visdom可以实现这个功能。
断点,数据存盘
梯度下降– gradient
-
分治的思想,如二分法,求极值,寻找最优值,
-
梯度定义:
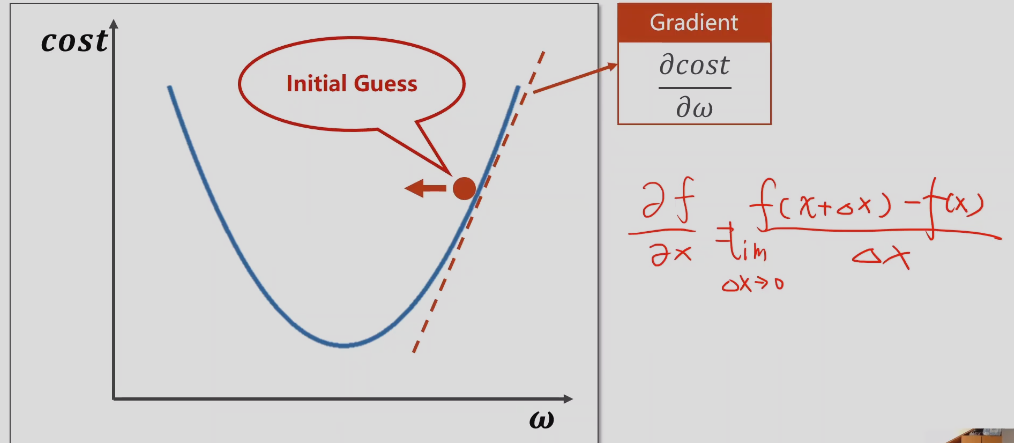

导数大于0,增函数,说明函数在上升
学习率表示往前走多远,值应该小一点,每一次迭代都朝着下降最快的反向前进
收敛: 模型刚开始训练的时候,cost损失会下降的非常快,但是越往后下降的越来越慢,说明模型训练过程趋向收敛。
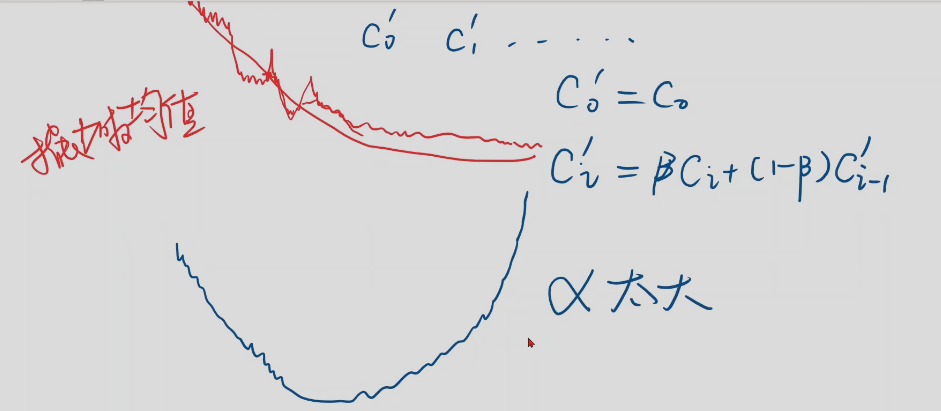
-
随机梯度下降
只需要求一次就可以,随机求一个样本
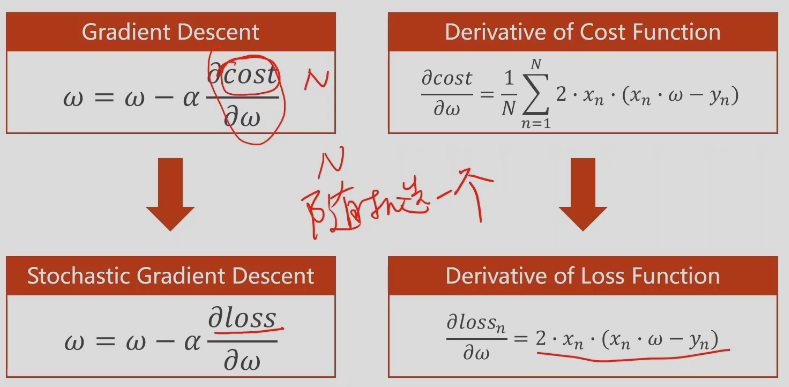
batch 梯度,兼具时间复杂度和性能
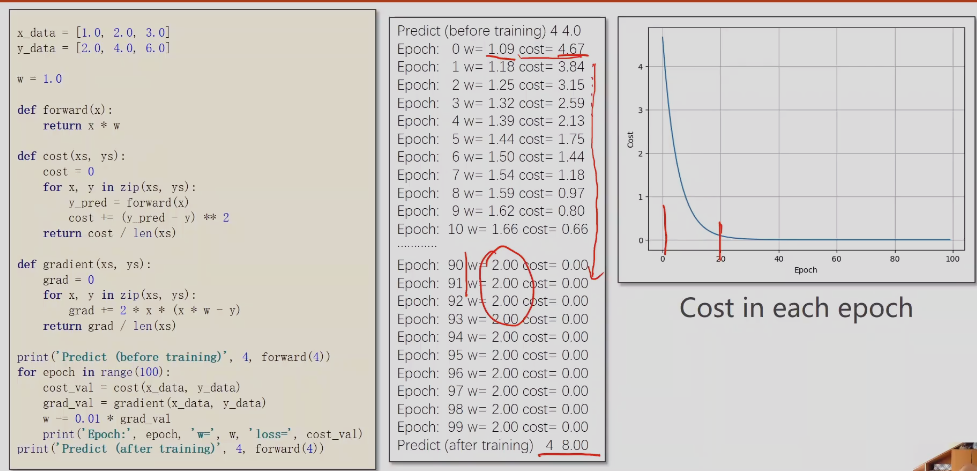
反向传播–back propagation
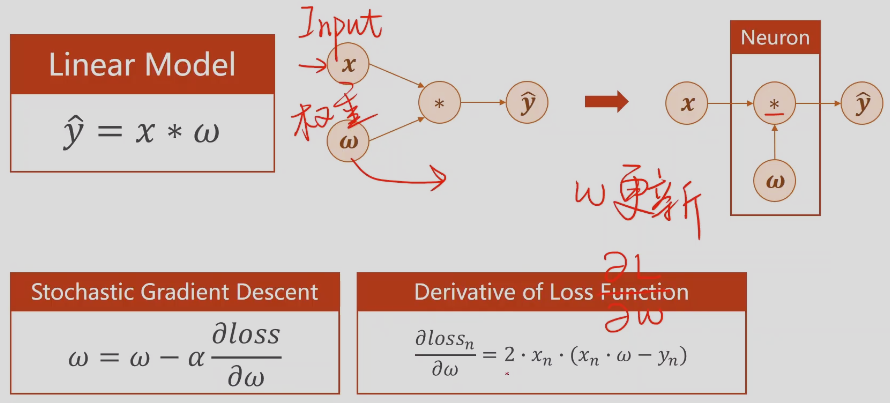
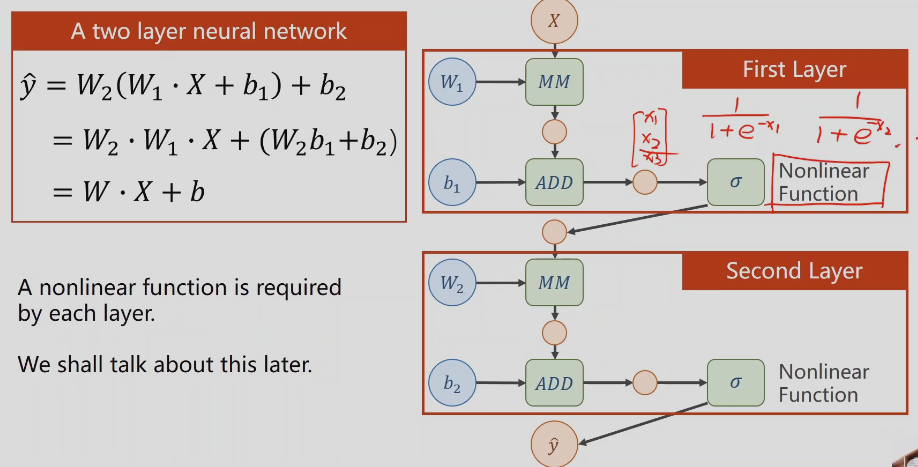
每一层输出需要加一个非线性的函数,
计算方法:
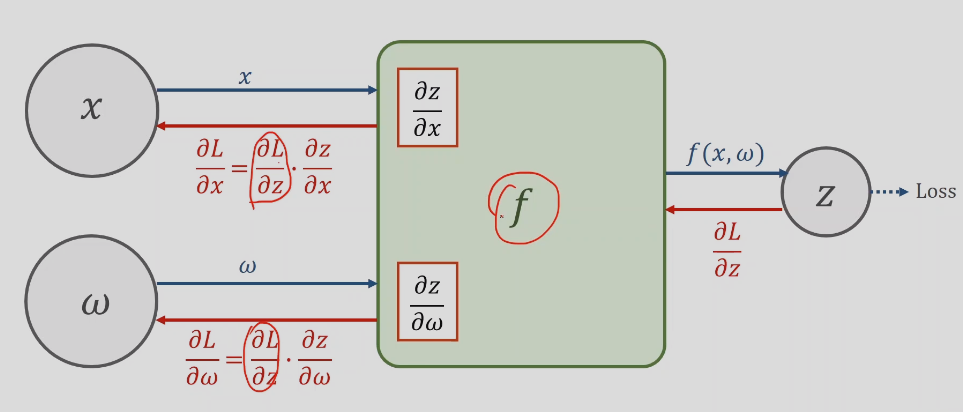
先前馈计算,源着箭头的方向计算,再反过来计算
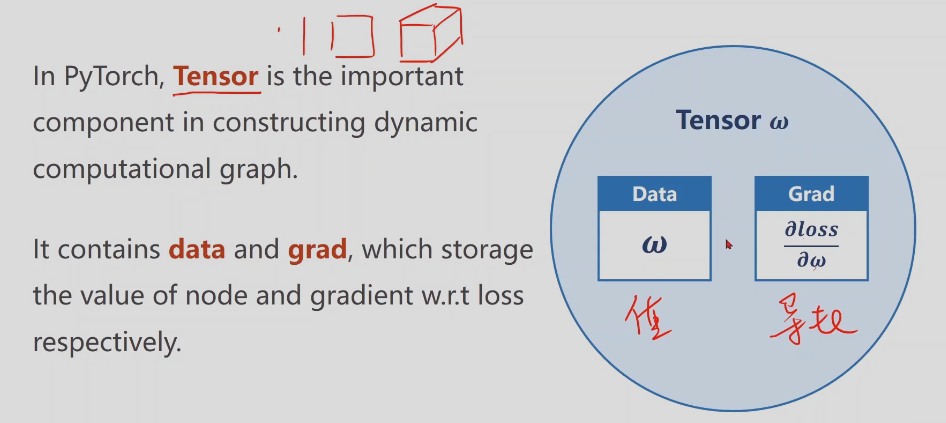
pytorch基本类型,Tensor是重要的数据存储单元,包含data(存权重)和grad(损失对权重的导数)


requires_grad默认为FALSE,需要设为TRUE才会计算梯度
w是Tensor矩阵形式,x也要是对应的矩阵,然后转换成计算图的模式

这个代码是在构建计算图
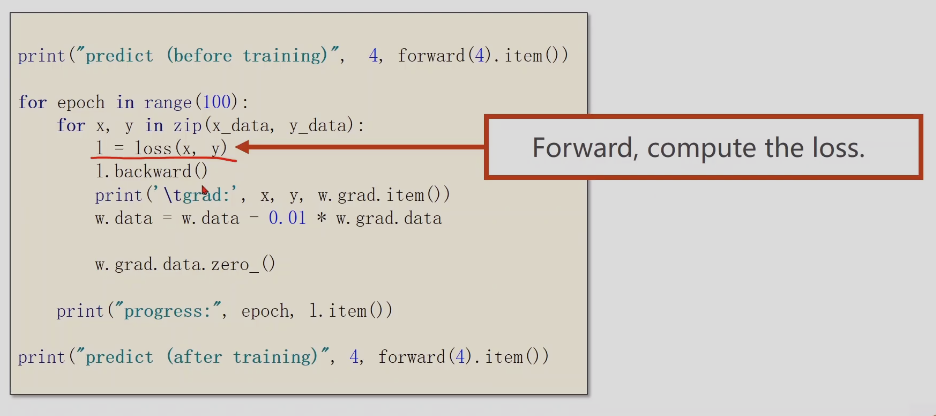
L = loss(x,y), 前馈计算,源着计算线路图计算loss,正向反馈计算损失
l.backward 是反向传播,反向计算计算图中每个变量的导数,并存入变量中,反向传播后计算图会被释放,这里计算w的导数
w.data = w.data - 0.01*w.grad.data
这里需要对data进行操作,grad也是Tensor张量,需要取data,否则张量计算就会生成计算图
l也是张量,不能直接加减
如:sum+=l.item() l是向量
w.grad.data.zero_()对w导数的值清零,如果不清零,第二次会保留w第一次的导数,结果就是两次导数的和
pytorch使用
-
Tensor 张量
-
forward
-
backward
矩阵乘法,行的每个值乘以另一个矩阵列的每个矩阵的值得和,
-
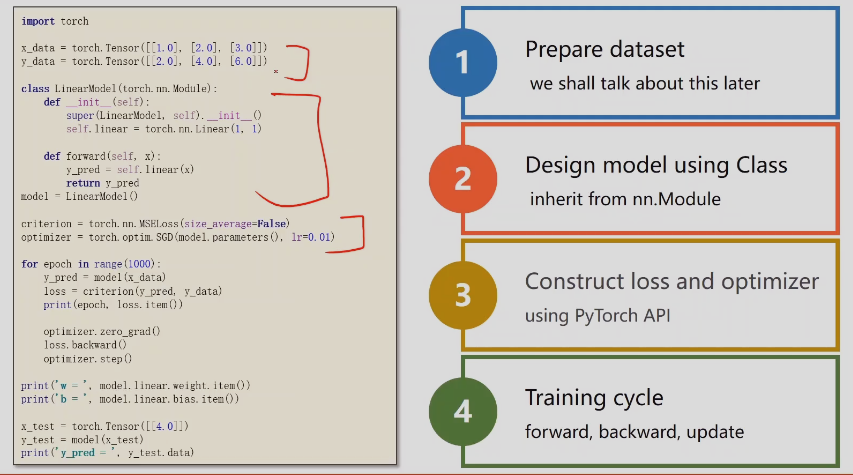
第一步准备数据
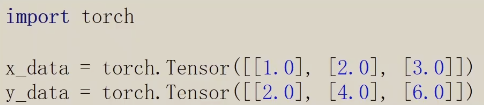
x、y必须是矩阵
-
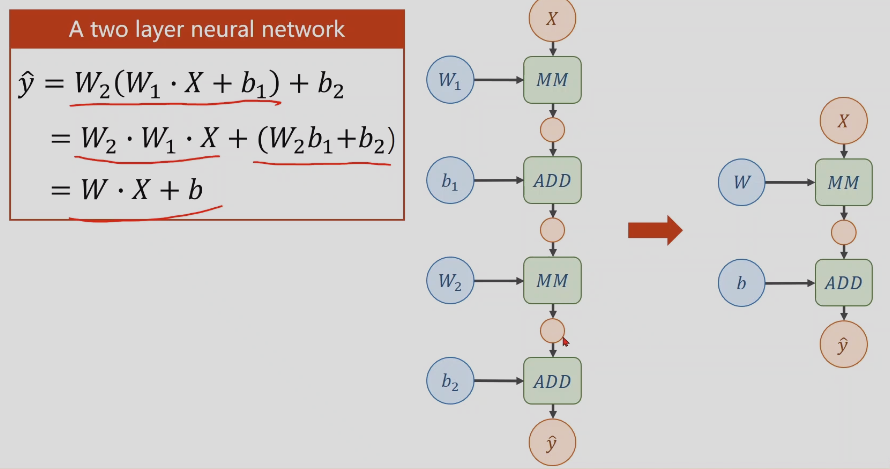
第二部设计模型
这里的模型(nn.Module)就是计算y_hat


-
构建损失模型和优化器

criterion需要参数y_hat和y;MSELoss和SGD都是类,criterion和optimizer都是这些类的一个实例化
model.parameters(),是调用模型linear.parameters中所有的参数;lr是学习率
-
训练循环
前馈(计算损失)、反馈(计算梯度)、更新(梯度下降算法更新权重 )
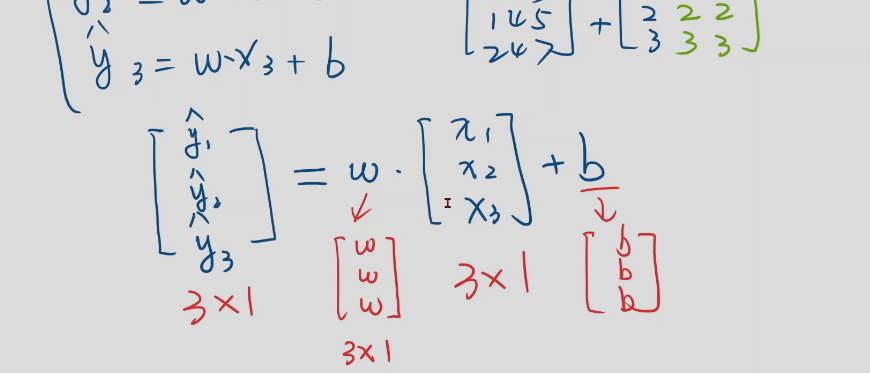
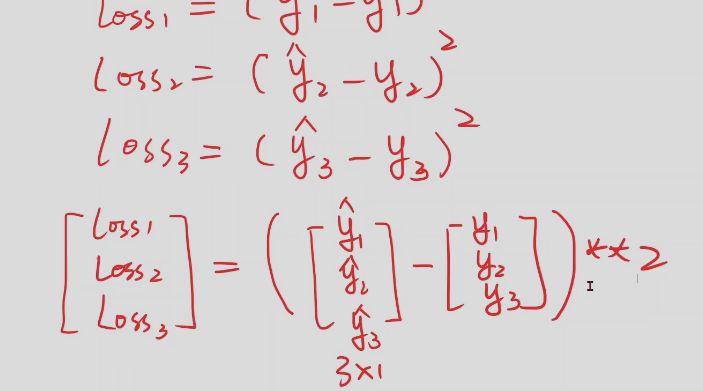
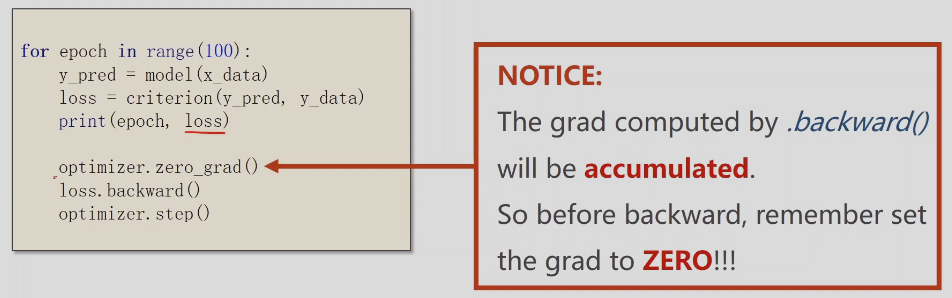
- 先算y_hat
- 再算loss
- 所有参数梯度归零
- 反馈
- 更新

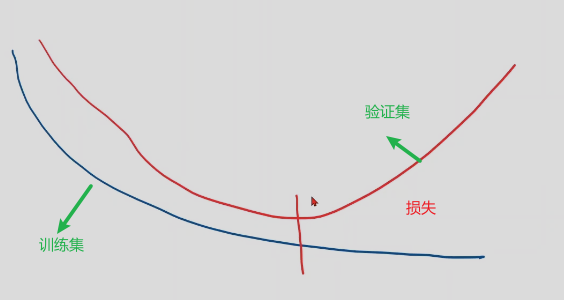
说明99次的时候,模型损失0.25,模型未收敛,效果不理想
999次时,模型收敛
模型不是训练越多越好,训练过多可能过拟合,在训练集上表现很好,但是在开发集的验证集上,损失反而上升,所以训练过程中需要关注开发集中损失有无上升
逻辑回归–分类问题
-
官方提供的一些流行的数据集–torchvison包

回归问题是关心最后考试能拿多少分,计算一个结果。
而回归问题关心能否通过考试,类别的概率的分布(通过与不通过),二分类问题,只用算一个类别的概率。因为两个类别的概率和必须为0,P(y_hat = 1)
-
逻辑回归原理
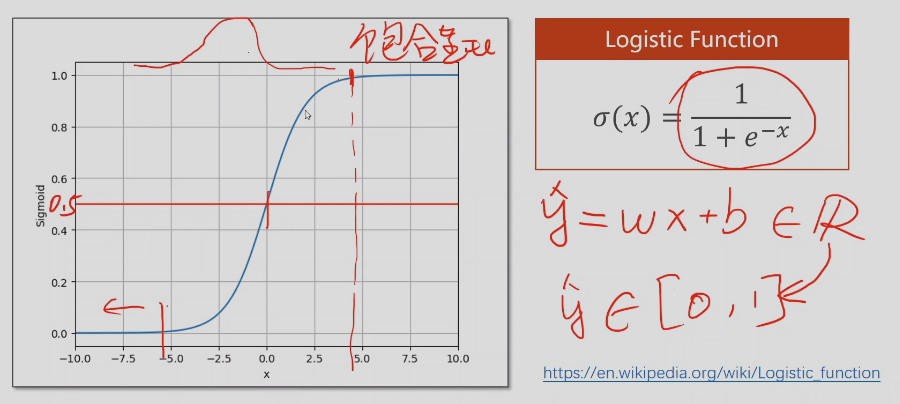
线性回归预测的结果值域是实数范围,而分类的概率值域是[0,1]的区间,需要把预测是实数值映射回[0,1],所以用到了上面的函数
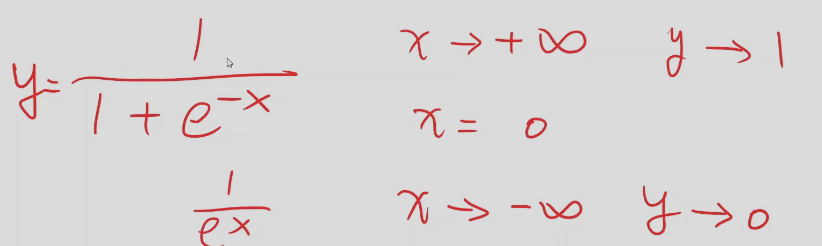
饱和函数:导函数大于0时,导数越来越小,趋于0
逻辑回归函数的导数接近于正太分布
逻辑回归函数可以保证值域在0~1之间

最终损失函数不是比较坐标轴中值得差异,而是概念分布的差异
cross-entropy交叉熵
多维数组
-
多维数组: 即有多个特征,多个变量x
-
mini batch

计算多维线性回归z的方法,矩阵运算
-
空间转换
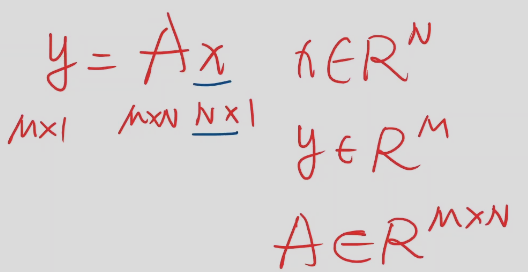
x是n维空间的任一向量,然后乘以A之后结果是m维度的空间里面,那么所乘矩阵是m*n的矩阵,它表示从n维空间映射回m空间的线性变换,矩阵是一种空间变换的函数

这个的意思是把任意8维空间的向量映射到一个成2维空间上,这里做一个线性映射。
但是我们经常要做的空间变换中,可能不一定是线性的,可能是一些非常复杂的非线性,所以我想用多个线性变换层,通过找到最优的权重,把他们组合起来,来模拟这种非线性的变换,神经网络本质是寻找一种非线性的空间函数
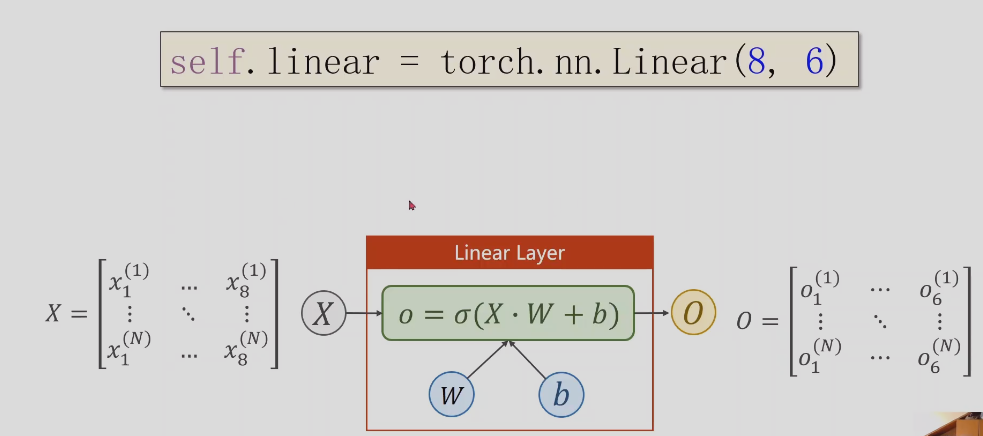
sigema可以把线性函数转换成非线性函数
深度神经网络中神经层数越多,学习效果很好,学习能力越好,但是并不是精度越高越好,精度太高也会把噪声学习,造成过拟合,所以模型需要泛化能力
读文档能力,基本架构能力(微机原理、cpu),开发的核心能力,这种方法泛化能力,将来遇到新的编程语言,可以快速读文档,快速上手。
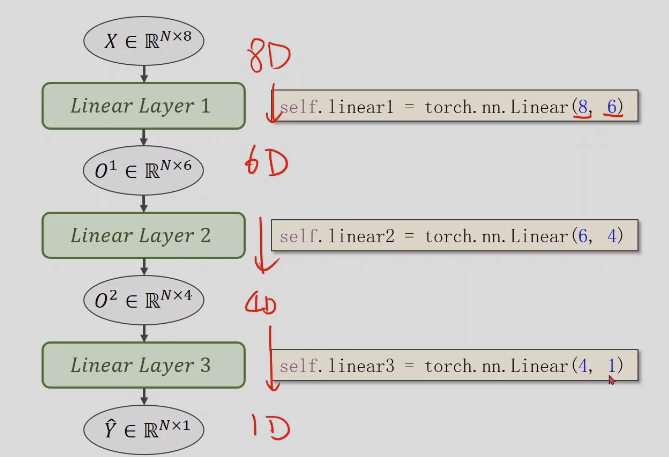
分多个层一步步降为,而不是直接从n维降到1维,可以找到更好的特征,层数越多,非线性越强,可以更好的学习分布。

np的loadtxt可以直接读入gz压缩文件;一般神经网络使用的是32位的浮点数,由于显卡的限制
这里[-1]拿出来的是矩阵,如果不加[]拿出来的是向量,计算的时候都要死矩阵,不能是向量
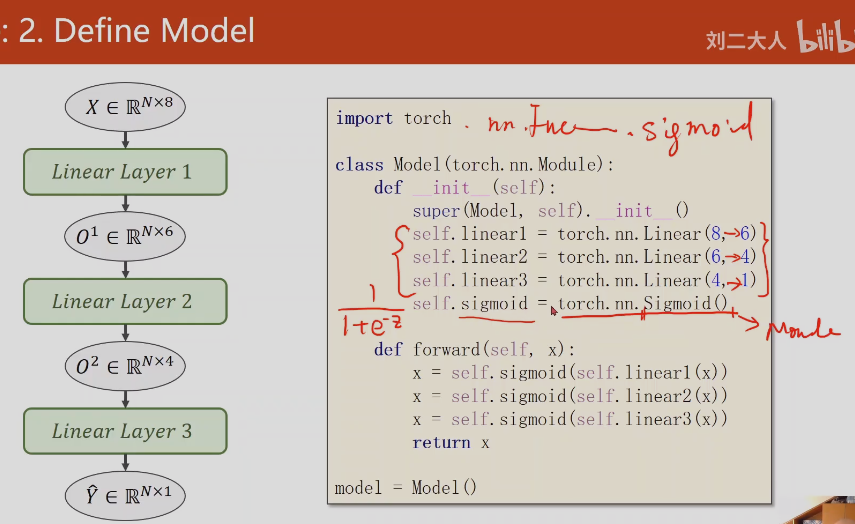
这里变量x都一直用一样的,方便调试,不容易出错,这里第一个x相当于是O1
加载数据集
Dataset和DataLoader
-
DataLoader是给数据集增加索引,方便拿取mini-batch的数据(也就是整个数据集中取部分用于训练,提高精度和效率,一般随机梯度下降,对于单个样本训练效果会最好,会获得比较好的随机性,帮助我们跨过鞍点,但是效率很低,对于整个数据集(一个batch)进行操作,很快,但是精度差),mini-batch均衡性能和效率的需求。
-
mini-batch

训练循环包含两重循环,第二层(内层)是mini-batch,外层是把所有mini-batch循环都跑一遍
Epoch
就是所有训练数据的一次前馈传播和一次反馈传播,也就是说把所有的样本都参与了一次训练
Batch-Size
每次训练的时候用的样本数量
Iterations
batch一共分了多少个,即内层跌代一共执行了多少次
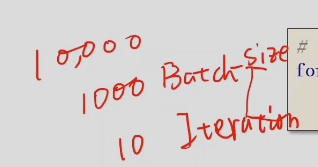
shuffle = True,每次训练的mini-batch使用的数据都是打乱顺序随机选择的
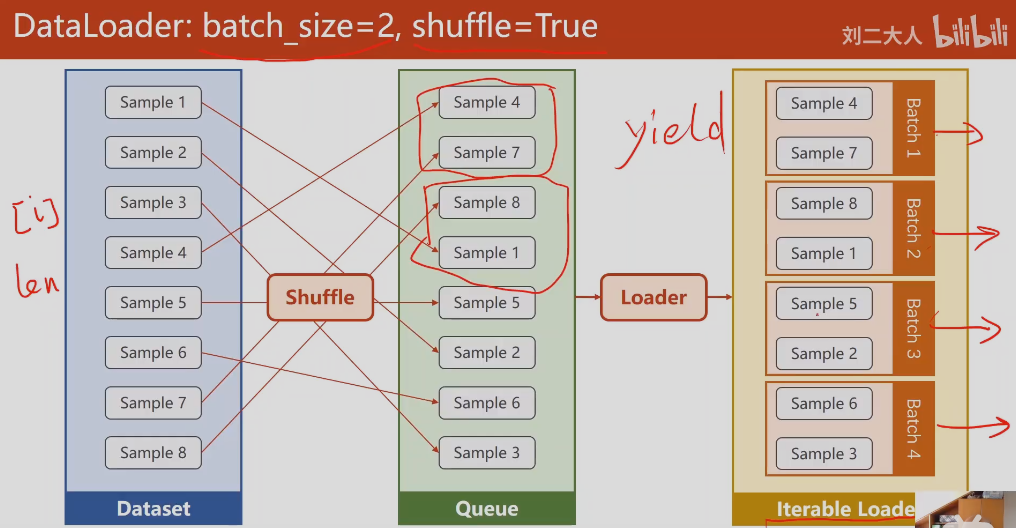
先shuffle打乱样本顺序,然后loader分组,这里batch-size=2,就两两分组

Dataset是抽象类,它不能被实例化,只能被其他类继承;Dataloader可以实例化
_getitem_作用,增加索引,支持下标操作;len支持数据条数返回
数据集如果本身不够大,可以使用第一种方式,一次性读入内存,
如果数据集很大,可以把数据集的文件名放到一个列表里
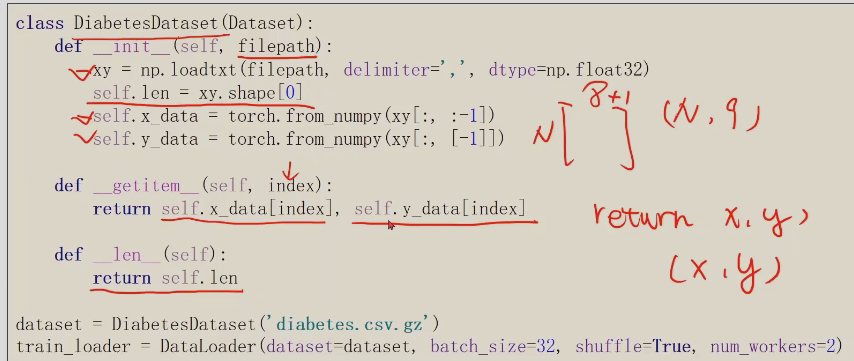
这里因为数据集很小,所以,直接把x_data,y_data直接加载到内存中,return x,y 返回(x,y)的元组


练习
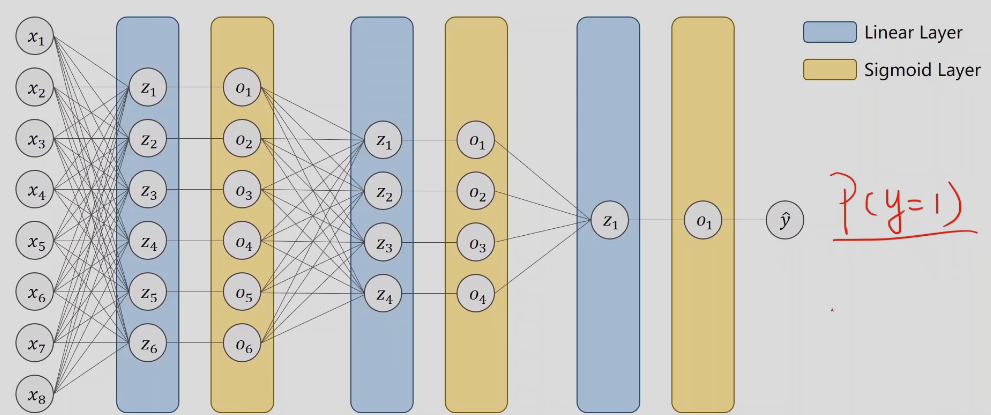
## 多分类问题–softmax layer

输出的每个值的概率需要满足:P>0; sum(P)=1
线性变换后的值有正有负,怎么通过变换都变成[0,1];
如何变换是和为1
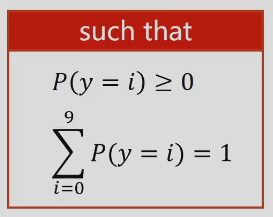

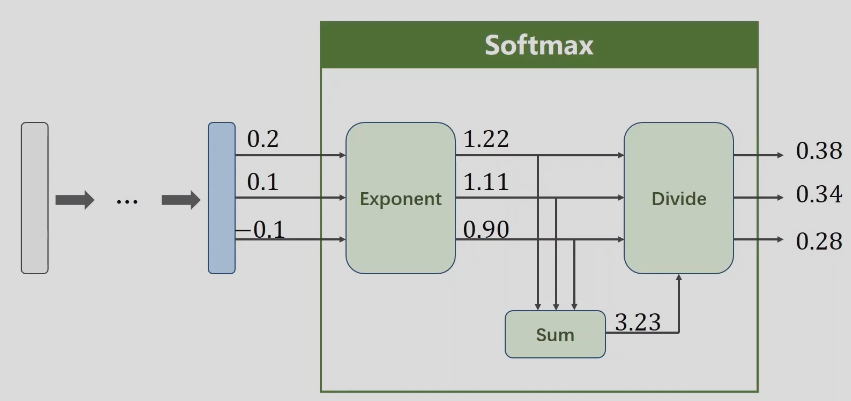
只有一步做softmax变换
2.计算损失函数–交叉熵 cross entropy

Loss(Y_hat, Y) = -YlogY_hat
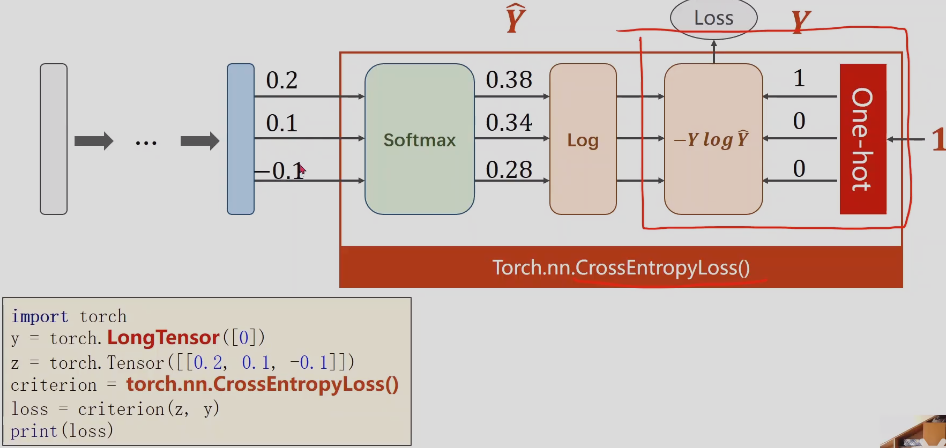
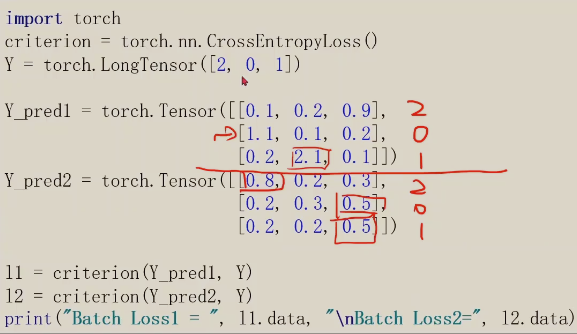
注意: 交叉熵损失,最后一步不需要做非线性变换,直接交给交叉熵损失就可以

python读入图像使用pillow
深度神经网络对于图像训练要求,图像需要转换成图像张量,像素值在-1~1之间,满足正态分布
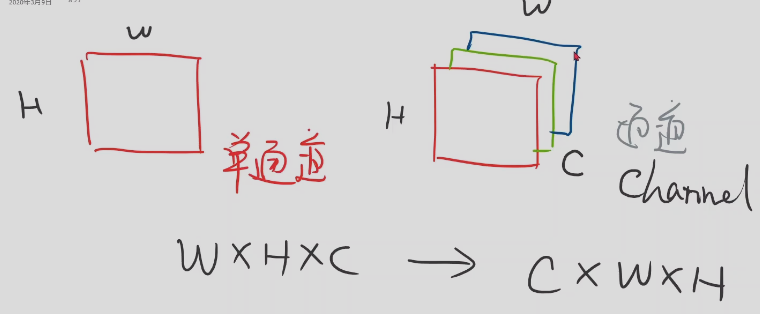
图像张量,单通道和多通道;pytorch需要将图像从W* H * C转换成C * W * H方便深度神经网络更高效操作图像

首先将pixel从[0,255]压缩到[0,1]; 然后将图像从单通道转换成多通道
归一化:
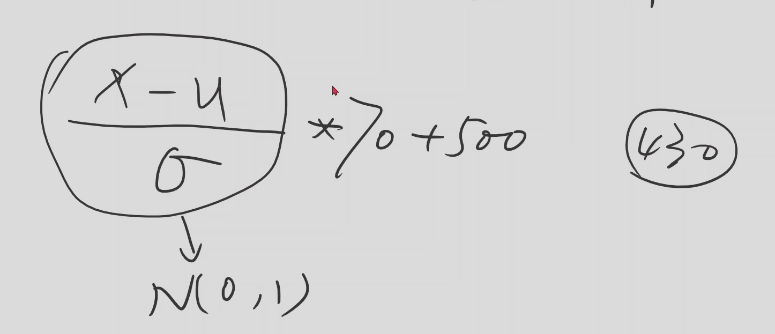
四六级成绩,先把成绩映射到了0~1分布里面
-
准备数据集

-
设计模型
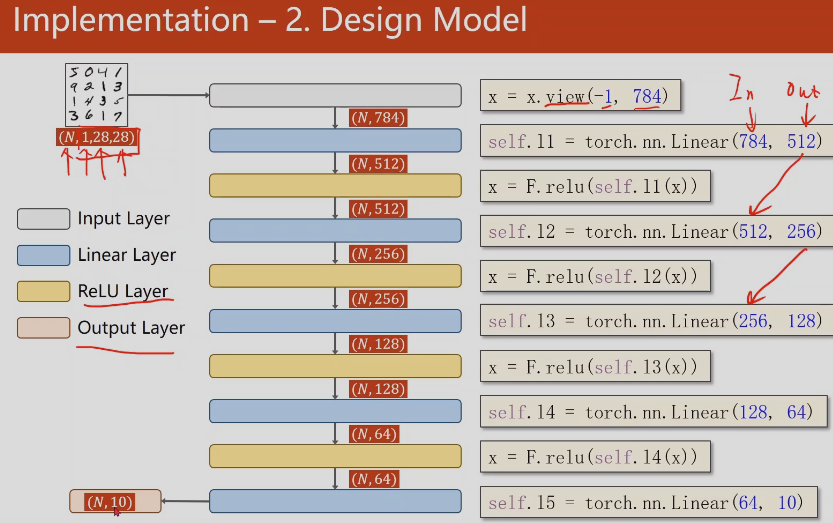
首先需要把1* 28 * 28的三阶张量变成一阶的向量;变换方法,把图像的每一行拼起来,这一行共有784个元素
view是改变张量的形状
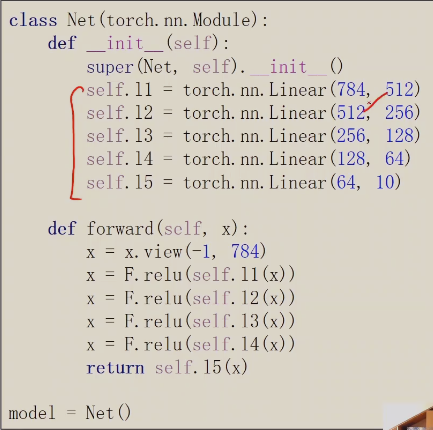
注意:最后一层不做激活
-
优化器

增加了冲量,相当于惯性,下山时速度更快
-
训练

optimizer.zero_grad()优化器使用之前应该先清零
取loss值时需要使用loss.item()
-
测试

torch.no_grad(),test不需要计算梯度
需要把每行最大值的下标拿出来
